2016考研数学：如何理解可导与可微？

备考指导来源：文都教育 2015-05-16　

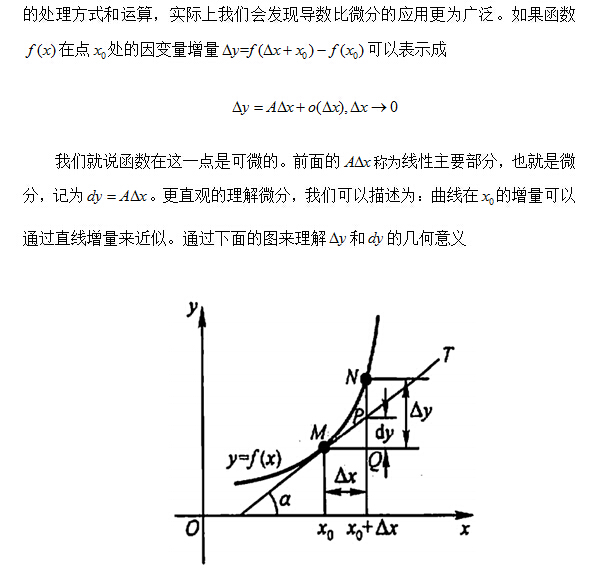
在学习了函数、极限以及函数连续性的概念之后，我们开始进入一元函数微分学模块的学习内容。高等数学又叫微积分，可见微分学在高等数学的学习中所占的重要地位。这一大块的内容我们按照以下四部分进行展开学习，可导与可微，导数的计算，导数的应用，以及中间穿插着学习中值定理。每接触一个新的模块，我们首先应该理解概念。在这里我们需要理解什么是可导什么是可微。

首先通过导数的两个实际背景，包括几何(切线斜率)和物理(速度或者扩展为变化率)背景去理解导数的定义。大家会发现，导数的本质就是极限。极限是高等数学中处理问题的一个核心思想。那么有关极限的性质就可以拿来刻画导数性质，例如左右导数的定义，导数存在的充要条件是左右导数存在且相等。类似函数连续的定义，从某点连续扩展到区间连续，我们也可以定义函数在开区间上可导，并且有了左右导数，我们可以继续定义函数在闭区间上可导。由此得出导函数的概念。这里需要大家注意，导函数也是一种函数，所有用来研究函数的性质和工具同样可以研究导函数，例如对导函数求极限、研究导函数的连续性、可导性等。导函数的导数我们称为高阶导数。以上是关于对导数定义的理解。

现在我们学习了函数的两个性质：连续性和可导性。那么这两者之间有什么关系呢?大家都知道这个定理：可导必连续。也就是题目中给出函数可导的条件，就隐含着告诉我们函数连续，关于这个知识点一般考察分段函数在某点可导，求参数取值，我们通常先讨论函数连续性，再讨论可导性。因为通过讨论连续性一般可以求出其中一个参数取值，方便后续可导性的讨论。比如下面这个例题

可导与可微